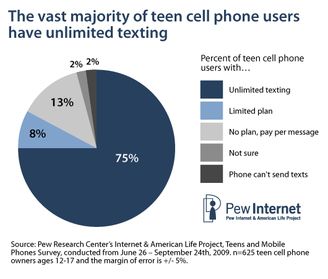
OMG, Unl. TXT FTW!!!
I like how this site uses a question posed by a student, akin to "How do I graph a function that has a changing slope?" The example quickly divulges to cell phone pricing structure, a valid place to go The issue I have with their example is that the majority of my students who have cell phones and an awareness of these pricing structures realize quickly how outdated the example is and lose engagement in the class discussion. Cell phones make calls, true; however, the majority of the usage my students' phones see is by text messaging, which most of them have a HUGE allotment of messages per month by their phone plan (many of whom will have unlimited texting anymore). So while the cell phone pricing examples are valid examples to introduce piecewise functions in a context familiar to students, they are quickly outdated by the rapidly changing face of technology today.
The Khan Academy example I found that lends itself to piecewise functions takes almost 3 minutes to get the example drawn on the screen (while Sal says twice "I hope I'm not boring you while I'm drawing this" and also "I really should have something that lets me just get the graph image in place quickly"). I have to be a bit lenient, though, because his video was posted in 2007 which is better than I was doing back then (I was, however, using a SMART Board regularly in daily class activity though and feigned a couple efforts at uploading my stuff).
Students become quickly detached from examples in their textbook and I would have a hard time justifying asking them to watch a 9-minute KA video where the first 3 minutes are setting up the example.
The Khan Academy example I found that lends itself to piecewise functions takes almost 3 minutes to get the example drawn on the screen (while Sal says twice "I hope I'm not boring you while I'm drawing this" and also "I really should have something that lets me just get the graph image in place quickly"). I have to be a bit lenient, though, because his video was posted in 2007 which is better than I was doing back then (I was, however, using a SMART Board regularly in daily class activity though and feigned a couple efforts at uploading my stuff).
Students become quickly detached from examples in their textbook and I would have a hard time justifying asking them to watch a 9-minute KA video where the first 3 minutes are setting up the example.
I visited the convenience store in town and compiled this photo (the one pictured above left) of their donut case, which indeed exhibits the characteristics for a piecewise function (while also allowing us to discuss the greatest integer function, since we can only purchase whole number quantities of donuts). I simply project the image in class when they come in and have already set the scene for the lesson, despite having to address the "So, we're taking a field trip today?" and "Did you bring snacks?" comments from students as they arrive. [NOTE: The amount of time showing this image in class should be inversely proportional to the amount of time to the nearest meal for your students.]
Have students create a price table for the quantity of donuts purchased, from 0 to about 15. They get an interesting surprise around the dozen-donut mark (namely that 11 donuts costs $10.44 and 12 donuts costs $9.99--so it is as if the 12th donut earns you a $0.45 refund!). These sort of conclusions are ones students treat as an inside joke among their other classmates, so don't sell it short despite the nerdiness it entails. Since we're supposed to help our students make real-world connections, this is a prime example--and a delicious one, to boot.
Have students create a price table for the quantity of donuts purchased, from 0 to about 15. They get an interesting surprise around the dozen-donut mark (namely that 11 donuts costs $10.44 and 12 donuts costs $9.99--so it is as if the 12th donut earns you a $0.45 refund!). These sort of conclusions are ones students treat as an inside joke among their other classmates, so don't sell it short despite the nerdiness it entails. Since we're supposed to help our students make real-world connections, this is a prime example--and a delicious one, to boot.
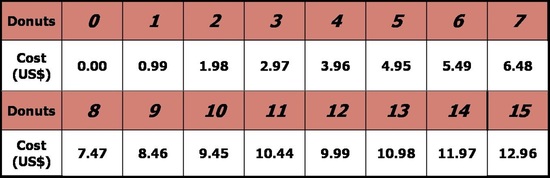
Krispy Kreme price chart. Have students construct it and see if they notice anything around the dozen-donut mark.
In the video examples I complete below using foldables, I try to emphasize that each of the PIECES of the function could stand alone by themselves with no restriction on their domain(s). With a piecewise-defined function, we are merely piecing together the parts of the individual functions that are requested in the piecewise function that DOES specify constraints on the individual component functions.
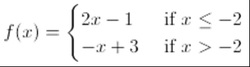
This is the example worked out in the YouTube video below. A copy of the foldable used for a 2-piece piecewise function can be found HERE.
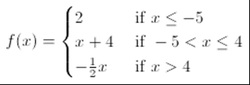
This is the example worked out in the YouTube video below. A copy of the foldable used for a 3-piece piecewise function can be found HERE.
Obviously, I need to develop a better way to make a quick demo of lessons like this. These were each done on my iPad2, so I'm pretty pleased with the capability of them to collect decent sound and video. What I did not show were the cue cards I created for myself just behind the iPad so I could more quickly graph and plot the functions (something Sal did not do on his example I mentioned earlier). Oh, and I included a shout out to Vi Hart for having used Sharpies for both of the videos. So, I've got that going for me, which is nice.
Piece, I'm outta here. Yes, I misspelled that. I meant to. Math puns are hard, I gotta take what I can get.
--Keltner--
Piece, I'm outta here. Yes, I misspelled that. I meant to. Math puns are hard, I gotta take what I can get.
--Keltner--
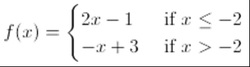
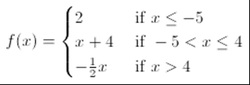
RSS Feed