
Allow me to dwell on the 24-hour time format a bit longer, with a military focus. Here are some phrases commonly heard (or slightly paraphrased) in movies associated with the military:
"Reveille is at 0500." Fine. I understand that. They blow the bugle at 5 a.m.
"Lunch at 1200." Gotcha, I know that means at noon. Just tell me where.

My mind thinks "How many hours past 1200 is that?" Therein lies an example of the importance of remainders.
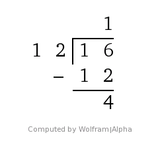
Whether students/soldiers/civilians/passersby realize or not, they have lunged headlong into a key concept in number theory: modular arithmetic.
I created (what I felt at the time was) a good introductory worksheet on modular arithmetic, using students' complaints about "always having the same thing for lunch" and made up a rotating set of dishes served in a neighboring school's cafeteria. A scan of the original, older version of it and the answer key is available HERE, if interested.
Symbolically, this tells us that 16 == 4(mod 12), or that when divided by 12, the numbers 16 and 4 have the same remainder. By similar measure, I could quickly determine that a football coach saying "kickoff is at 1900" is not just due to the fact he is a social studies teacher and currently talking about the 1900's in U.S. History class. Since 19 == 7(mod 12), he is referring to 7:00 p.m. for kickoff time.
But remainders go beyond just telling time. Suppose today is the 5th and I need to know what day of the week the 19th falls on? You may not use the word "remainder" but somewhere in your logic, the concept does rear its head at you. Admit it.

- You are in line at the store and an item's bar code does not scan, so the clerk enters the UPC manually, only to receive an "Invalid UPC" prompt on their register.
- You need to order a textbook for a graduate course, but find the book title, subtitle, edition, author(s), publisher, and publish date to be an exhaustive list of information to compile to verify you order the appropriate book.
- You are baffled by the small series of tick marks that appear on junk mail you receive, but have a hunch it helps automatic sorters at the Post Office begrudgingly deliver those items in a quick, efficient manner without having to read your misspelled name and incorrect address or, my favorite, "Or Current Resident" on the name line.
These are all valid applications of UPCs, ISBNs, and IMBs; and no, that's not a competition for more acronyms than you'll hear in a staff meeting about NCLB, CCSS, or SBG.
I tend to focus here on UPCs and ISBNs, because they are the most readily available examples I use in class when a student brings up this topic. Not once have I been interrupted with a "Do we need to know this for the test?" I like to think it is because students are engaged in the topic, since it is applicable to a plethora of things around them.

"UPC" stands for Universal Product Code. UPC bar codes were originally created in 1973 and are still maintained by a company called the Uniform Code Council (UCC) in Dayton, Ohio. They were originally made to help grocery stores speed up the checkout process and keep better track of inventory, but the system quickly spread to all other retail products because it was so successful. Now, they become commonplace and are used by health care providers, at the library, and even for ticketing at sporting events.
UPCs originate with . A manufacturer applies to the UCC for permission to enter the UPC system. The manufacturer pays an annual fee for the privilege. In return, the UCC issues the manufacturer a six-digit manufacturer identification number and provides guidelines on how to use it. You can see the manufacturer identification number in any standard 12-digit UPC code. The UPC symbol has two parts:
- The machine-readable bar code
- The human-readable 12-digit UPC number
The last digit of the UPC code is called a check digit. This digit lets the scanner determine if it scanned the number correctly or not. Here is how the check digit is calculated for the other 11 digits, using the code 41539984380 from my Dillon's Plus Shopper's Card pictured above (I use it because if anyone steals the code, then the only backlash will be racking up fuel points more quickly, earning an even bigger discount on gasoline) :
- Multiply the numbers in the odd positions times 3 and add the resulting products together (great example of the distributive property available for the taking, if you do this in class).
- Add the numbers in the even positions (in essence, multiplying by 1).
- Combine the sums from Steps 1 & 2 above.
- Divide the total in Step 3 by 10. Ten minus the resulting remainder is the check digit (12th and final digit) for the UPC.
- 3 * (4 + 5 + 9 + 8 + 3 + 0) = 3 * (29) = 87
- (1 + 3 + 9 + 4 + 8) = 25
- 87 + 25 = 112
- 112 / 10 = 11 remainder 2. Hence, (10 - 2) = 8 and 8 is the check digit, as pictured above.
Some further investigation allowed me to discover the leading value is actually an indicator of the code's Number System. The Number System (NS) is the first digit in the UPC and is used to identify the type of product being coded.
| NS Description 0 Regular UPC Code 1 Reserved 2 Weight Items 3 Drug / Health Items 4 In-store use on non-food items | NS Description 5 Coupons 6 Reserved 7 Regular UPC Code 8 Reserved 9 Reserved |

The original ten-digit ISBN-10 format, in use for more than 30 years, was officially replaced with a thirteen-digit ISBN-13 beginning in January, 2007.
The first "group" (hyphenated section of numbers) in ISBN-10 or second "group" ins ISBN-13 is a single digit which encodes the country or language in which the publisher is incorporated: 0 & 1 for English, 2 for French, 3 for German, 4 for Japanese, 5 for Russian, 7 for Chinese, and 8 for Indian publishers, to name a few.
The next group of digits specifies the publisher, and may range in length from two to seven digits, with fewer digits reserved for larger publishers (great example of inverse variation here).
The next group of digits specifies an individual book, taking between one and six digits to do so. Small publishers have the ability to encode as few as 10 books, while larger publishers can encode as many as 1,000,000 books.
The last digit is a check digit which may be in the range 0-9 in either ISBN-10 or ISBN-13, or use an "X" (the Roman numeral for 10) with ISBN-10 since its check digit is determined by division by 11. The check digit is computed as indicated below for each ISBN format:
ISBN-10:
- The number has 9 information digits and ends with 1 check digit.
- Assuming the digits are "abcdefghi-j" where j is the check digit. Then the check digit is computed by the following formula:
- ISBN-13 has always been prefixed with "978", which are backwards-compatible and able to be converted to ISBN-10.
- Now, "979" is coming into use and is not able to be converted to ISBN-10, further enforcing the transition to ISBN-13.
For the ISBN-10 pictured earlier (actually from the Algebra 2 textbook I currently use), its ISBN 0-618-59541-4, we get:
j == ( [0 6 1 8 5 9 5 4 1 ] * [1 2 3 4 5 6 7 8 9] ) mod 11
== ( (0 * 1) +(6 * 2) + (1 * 3) + (8 * 4) + (5 * 5) + (9 * 6) + (5 * 7) + (4 * 8) + (1 * 9) ) mod 11
== ( 0 +12 + 3 + 32 + 25 + 54 + 35 + 32 + 9 ) mod 11
== ( 202 ) mod 11, and since 202/11 has a remainder of 4, the check digit, or 10th digit, for this ISBN is 4.
ISBN-13:
• The number has 12 information digits and ends with 1 check digit.
• Assuming the digits are "abcdefghijkl-m" where m is the check digit. Then the check digit is computed by the following formula:
m = 10 - ( [a b c d e f g h i j k l] * [1 3 1 3 1 3 1 3 1 3 1 3] ) mod 10
For the ISBN-13 pictured from Marvin Bittinger's book "The Faith Equation, 978-1-59755-254-7, we get:
m = 10 - ( [9 7 8 1 5 9 7 5 5 2 5 4] * [1 3 1 3 1 3 1 3 1 3 1 3] ) mod 10
m = 10 - ( (9*1) + (7*3) + (8*1) + (1*3) + (5*1) + (9*3) + (7*1) + (5*3) + (5*1) + (2*3) + (5*1) + (4*3) ) mod 10
m = 10 - ( (9) + (21) + (8) + (3) + (5) + (27) + (7) + (15) + (5) + (6) + (5) + (12) ) mod 10
m = 10 - ( 123 ) mod 10 and since 123/10 has a remainder of 3,
m = 10 - 3 = 7, so the check digit, or 13th digit, for this ISBN is 7.
Despite having a very small niche for an audience, I have come to appreciate the number theory necessary to unravel these seemingly simple systems in life around us.
If I launch into a discussion of this caliber in class, I try to lighten the mood by including a "You can impress your friends if you bring this up in conversation" or "I think this was a topic on Jeopardy last week, so you could win some money someday if you can remember it" to give students some sort of a lighthearted rationale for taking in information on a topic that is not necessarily going to "be on the test," as so many will inquire of me mid-sentence on more than one occasion.
On a side note, I mentioned the Marvin Bittinger book "The Faith Equation" earlier, which Bittinger actually gave to me himself, after I had a chance to meet him at a conference in October, 2011. He is a fascinating man and had a great opportunity to talk baseball with me after his presentation, even pulling out his iPhone to show Bob Feller as one of the contacts on his phone. Bittinger still takes part in fantasy baseball camps on a regular basis, even into his seventies, and was the person who prompted me to begin using Twitter.
Not long after having met Dr. Bittinger in person, I had the chance to meet Dan Meyer. I have a hard time conveying to my students (and my wife, for that matter) just how startstruck I was in meeting these two gentlemen and what an important role that play in the world of mathematics education.
I hope you learned something you did not previously know about number theory, coding strategies on retail items, and a bit of insight into military time structure. I better wrap this up for now. It's past 2200 hours and I have an early morning in my future.
--Keltner--
 RSS Feed
RSS Feed