 The "after-math" of introducing systems of equations. Delicious pun, huh? Introducing systems of equations about the same time of year as Halloween candy flows freely can be dangerous. I tried to use students' sugar cravings to introduce the topic in class though. I have a sweet spot for Little Debbie's Oatmeal Creme Pies and noticed a peculiar pricing setup betwixt their Single Decker and Double Decker snacks. At a budget-friendly price, I was able to bring snacks for my students to help solidify their work on the example we posed to introduce systems of linear equations. Gimmicky, I know, but it definitely grabbed their attention, wondering why I brought snacks that day.
 The rest of the example relied heavily on the photo at left, which showed two different "recipes" of Oatmeal Creme Pies available at our local convenience store, one the traditional Single-Layer-O'-Creme and the other the legendary Double Decker. This gave students a familiar context and placement of the example and led to a pretty casual conversation that was more engaging than cracking open the textbook, without a doubt. We investigated several things about the snacks: - Does the weight matter for the price (hinting at a use of direct variation which we had studied previously)?
- What are the things about the snacks we CAN change and which things are non-negotiable? (i.e. what are our variables and our constants in this scenario? I was proud they got this outlined so quickly.)
- Is there a more efficient way to solve for the cost per cookie layer and cost per creme layer?
So, with hook baited, we entered into the strategies for solving linear systems of equations, notably in this instance the substitution method. We set up the system of equations at the bottom of the graphic at left and solved, arriving at an astonishing revelation: The creme layer costs ZERO cents!(The cookie layer costs twenty-five cents, as we discovered.)Students had a hard time wrapping their heads around this, thinking more of the context or production costs until another classmate emphasized that our goal was to figure out the PRICE for each cookie and creme layer, not the COST.This was a decent introduction to the idea of a solution for a system of equations, because students emphasized to one another that zero cents for a creme layer did not make much sense on the surface, but the pricing structure we solved for WORKED with the label price of each snack (made a true statement). When I had to back up and give a concrete definition for what a solution to a system is, students had already seen it used in context and had a more concrete understanding of how it worked in the abstract sense of the topic.I hope you enjoy this example as much as my students did. Without a doubt, timing during the school day was critical with this example. Oh, a side note: I did not use the Oatmeal Creme Pies as pictured; I bought 12-packs that were a bit smaller but still grabbed students' attention just as well. For now, I need to run. Just reflecting on this lesson is making me hungry.
--Keltner--
 Students grew curious of this binary clock. A student approached me last week about a clock he had seen online, a binary clock (Link redirects to ThinkGeek where it was originally discovered) and was curious about how it could be read. I was able to fall back on a worksheet I created my first year of teaching, meant to be sort of a reading assignment (because at that time, our building was focusing on reading comprehension among our students). Granted, I definitely need to edit this lesson and include some better images and examples, as well as expanding upon the idea of how to "carry digits" when working in a base-2 system. Most of the emphasis on the worksheet is placed on how to convert from base-2 (binary) to base-10 (decimal) and vice versa though.
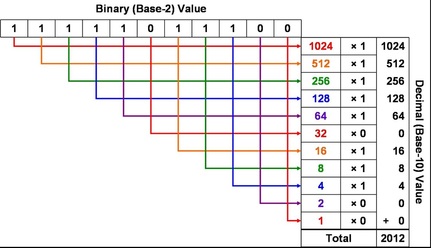 My new, edited visual aid to convert from base-2 to base-10. I've modified the table/chart from my worksheet mentioned earlier to the one at left. Our students attended Math Day at Emporia State University (my alma mater) on Ocotber 31, and one of the questions during the competition was: "Write 2012 in binary form."Luckily, my students had access to a TI-Nspire CX CAS which has a quick function to allow them to make the conversion, but they came away from the contest wanting to know more about how binary numbers work and if other similar systems exist. Another crowning achievement through all this discussion is that students understand the t-shirt design I have posted at the back of my classroom that says "There are 10 types of people in the world: those who understand binary and those who don't."--Keltner--
 I am not of Griswold heritage, thank you. Yup, I'm "that guy" in the neighborhood who puts up Christmas lights on the house the weekend after Halloween. Contrary to popular belief, though, I do it out of planning for inclement weather conditions that seem to come soon after November begins. While my daughters appreciate seeing our lights on, they also enjoy helping out with putting them on the house. Hence, the picture at left of my second daughter and I, properly footing a ladder. That's a term I learned through my firefighter classes, and also learned the proper angle for ground ladders of this type. The rule of thumb for proper ladder angle says: - If you can stand at the base of the ladder and reach out to the rung directly in front of your shoulder, the ladder is at a proper angle if you touch somewhere on the palm of your hand (to allow a little bit of room for error).
- If the ladder is positioned somewhere on your forearm, it is too steep and poses a safety hazard.
- If the ladder is so shallow that your fingers cannot reach it, the ladder will flex under the weight of the user and increase the potential for collapse of gutters or other objects at the other end of the ladder.
So I made sure to superimpose figures on the photo of me and wee-me to display the similar triangles that occur, but also to show the relationship of slope and how it relates to three collinear points along the ladder. [NOTE: The fact that my arm and duaghter's arm are not fully extended is due to the fact we stood PRECISELY at the base of the ladder instead of lining up our toes with the base. This was because I wanted to illustrate the slope more directly and not have to account for shoe size, although we both wear size 11 right now, just different categories.]
 Proper Ladder Angle should be at a 4-to-1 ratio (slope). The diagram at left also illustrates proper ladder angle, but does not include the ladder extending above the surface it is leaning on. The other feature I must point out is the user's feet are AT the ladder's feet, not lined up at the ankle's as my daughter's and my ankles were in the photo above.
While I'm not dwelling on a whole lot of math within this post, there are a lot of different directions a teacher can go with this: similar triangles and slope are just a sample.
Moreover, I would hope you get a little grin on your face as the holiday season arrives in the coming days, weeks, and month(s).
We definitely have a hefty glow at our house now. And yes, our lights did work the first time I plugged them in.
--Keltner--
 Click for Red Bull Stratos mission website. For the casual observer--well, hang on--no one casually observed Felix Baumgartner's jump from the edge of space on October 14th, 2012. Not everyone who watched had their mind racing like mine was, but I am certain that this feat is one more than befitting of #101qs and #3Acts formatting. What follows on this post is what I have managed to use in my own class to help quench students' curiosity about the Red Bull Stratos project, which sent a helium-filled balloon up to 128,100 feet and had Austrian skydiver Felix Baumgartner jump back to the Earth wearing a pressurized suit.
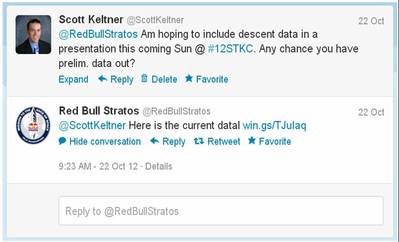 I got a response back from Red Bull Stratos! This coming Sunday morning, I will be presenting at the STEMtech Conference in Kansas City and was hoping to use an example from the Red Bull Stratos jump within my talk to show how velocity, acceleration, deceleration, and time can relate to one another--both for the balloon's ascent and Felix's descent back to the Earth. So, I tweeted the Red Bull Stratos folks. With 240,000+ followers, I figured it had fallen on deaf ears (although, since they're used to travelling faster than the speed of sound, they could use "I couldn't hear you" as a valid excuse). Nevertheless, I set out to collect some data points for use on the TI-Nspire CX using the Teacher Software. Below is a slide show of some of the work I completed. What I hoped students would take away from these graphs included: - The balloon appears to make a fairly constant ascent, but careful inspection would reveal the upward velocity of the balloon actually varied much more than at first glance.
- Does the elevation vs. time graph of Felix's descent convey enough information for us to know when he deployed his parachute? (This would be a great time to introduce the idea of a secant line to students, as a BRIEF introduction to a Precalculus and Calculus topics such as average rate of change and limits)
- Does the velocity vs. time graph of Felix's descent show enough to let us identify when he is accelerating and decelerating, when his parachute was deployed, and when he touched earth again?
Also, I'm including a link to the data I used to compile this activity on this post both as a Google Docs Spreadsheet and a Microsoft Excel file, and also the TI-Nspire CX document used here (this can be downloaded, then viewed within the TI-Nspire Document Player without needing software purchase or download of trial versions). Please use either however you see fit and let me know how it works for your class. The ascent data was gathered from this post on Wikipedia. The descent data was gathered by watching and pausing this YouTube video a couple different times (NOTE: these were approximate velocities and subject to verification and should not be considered 100% accurate, but did work well enough to conduct the lesson I was looking to convey).
 Click for more information on the Red Bull Stratos balloon. The other information I wanted to include in this lesson, but did not focus on in this lesson, included facts and figures about the balloon used in the Red Bull Stratos mission. At lift-off, the balloon was nearly 200,000 cubic feet (or 100,000 Giant Jenga games, as I was able to illustrate with my students in class, since we recently worked with it). At its highest point, the balloon was nearly 30,000,000 cubic feet large (which I related to my students by having them envision a cube that is as long, wide, and tall as a football field--a cube with side lengths about 310 feet on a side). Check this blog post on how the balloon compares with the Statue of Liberty When we approach a lesson that involves transformations of solids (impact on volume and surface area when a single dimension is altered), I will likely revisit this topic again with a different focus in mind. As much energy as my students brought to this lesson, then finding out that there were over 8 MILLION simultaneous YouTube viewers of the Red Bull Stratos mission (which was not mentioned on the mission's blog post among the other records and noteworthy feats achieved), I knew that this was a topic that would grab their attention. I also know how much my own mind was racing as I was watching the broadcast of the mission, so to leave it alone would be unheard of. But when the speed of sound was broken during the fall, that is the play on words I was hoping for: "unheard of." Mission accomplished. Thank you for being a great example to our students, Felix Baumgartner! Wait! An example in a lesson, I'm not saying that all our students should go jump in balloons and take up this sort of skydiving! There. I have to cover that segment of the population that will try and one-up this record by any means necessary. --Keltner--
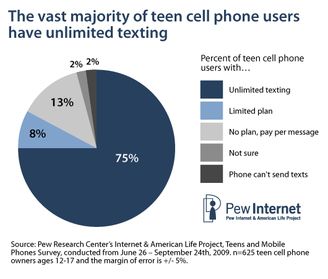 OMG, Unl. TXT FTW!!! I like how this site uses a question posed by a student, akin to "How do I graph a function that has a changing slope?" The example quickly divulges to cell phone pricing structure, a valid place to go The issue I have with their example is that the majority of my students who have cell phones and an awareness of these pricing structures realize quickly how outdated the example is and lose engagement in the class discussion. Cell phones make calls, true; however, the majority of the usage my students' phones see is by text messaging, which most of them have a HUGE allotment of messages per month by their phone plan (many of whom will have unlimited texting anymore). So while the cell phone pricing examples are valid examples to introduce piecewise functions in a context familiar to students, they are quickly outdated by the rapidly changing face of technology today. The Khan Academy example I found that lends itself to piecewise functions takes almost 3 minutes to get the example drawn on the screen (while Sal says twice "I hope I'm not boring you while I'm drawing this" and also "I really should have something that lets me just get the graph image in place quickly"). I have to be a bit lenient, though, because his video was posted in 2007 which is better than I was doing back then (I was, however, using a SMART Board regularly in daily class activity though and feigned a couple efforts at uploading my stuff). Students become quickly detached from examples in their textbook and I would have a hard time justifying asking them to watch a 9-minute KA video where the first 3 minutes are setting up the example.
 I visited the convenience store in town and compiled this photo (the one pictured above left) of their donut case, which indeed exhibits the characteristics for a piecewise function (while also allowing us to discuss the greatest integer function, since we can only purchase whole number quantities of donuts). I simply project the image in class when they come in and have already set the scene for the lesson, despite having to address the "So, we're taking a field trip today?" and "Did you bring snacks?" comments from students as they arrive. [NOTE: The amount of time showing this image in class should be inversely proportional to the amount of time to the nearest meal for your students.] Have students create a price table for the quantity of donuts purchased, from 0 to about 15. They get an interesting surprise around the dozen-donut mark (namely that 11 donuts costs $10.44 and 12 donuts costs $9.99--so it is as if the 12th donut earns you a $0.45 refund!). These sort of conclusions are ones students treat as an inside joke among their other classmates, so don't sell it short despite the nerdiness it entails. Since we're supposed to help our students make real-world connections, this is a prime example--and a delicious one, to boot.
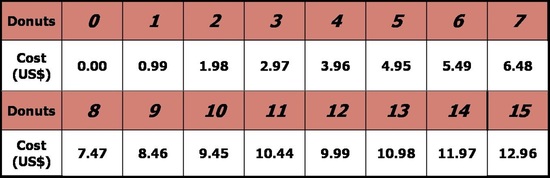 Krispy Kreme price chart. Have students construct it and see if they notice anything around the dozen-donut mark. In the video examples I complete below using foldables, I try to emphasize that each of the PIECES of the function could stand alone by themselves with no restriction on their domain(s). With a piecewise-defined function, we are merely piecing together the parts of the individual functions that are requested in the piecewise function that DOES specify constraints on the individual component functions.
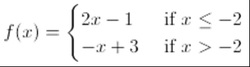 This is the example worked out in the YouTube video below. A copy of the foldable used for a 2-piece piecewise function can be found HERE.
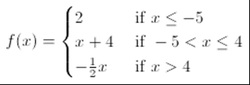 This is the example worked out in the YouTube video below. A copy of the foldable used for a 3-piece piecewise function can be found HERE.
Obviously, I need to develop a better way to make a quick demo of lessons like this. These were each done on my iPad2, so I'm pretty pleased with the capability of them to collect decent sound and video. What I did not show were the cue cards I created for myself just behind the iPad so I could more quickly graph and plot the functions (something Sal did not do on his example I mentioned earlier). Oh, and I included a shout out to Vi Hart for having used Sharpies for both of the videos. So, I've got that going for me, which is nice. Piece, I'm outta here. Yes, I misspelled that. I meant to. Math puns are hard, I gotta take what I can get. --Keltner--
 Doctor-approved backpack weight? I came to our lesson on linear inequalities in two variables, which coincidentally closely follows our discussions on direct variation, scatter plots, and linear regression. I wanted to find a unique real-world application for the lesson that tied these two topics together. I found a blog post for the New York Times wellness section that gave a decent path HERE: the relationship between student body weight and their backpack weight. The American Academy of Pediatrics recommends the student's backpack " never weigh more than 10 to 20 percent of your child's body weight." Consumer Reports insists that a backpack weigh no more than 10% of the student's body weight (I feel it necessary to point out that the emphasis of their claim seemed to be focused on elementary school-aged students; their insistence seemed to loosen up on secondary students, citing that their back muscles are stronger at those ages and better fit for a bit more extreme load). So, enter the lesson, sans the lab coats and clipboards that the Consumer Reports folks might have access to, and determine: Are my students' backpacks in compliance with the most extreme of these doctor recommendations?
I've created several activities that are intended to accompany this activity. Here are some of them: - TI-Nspire CX activity [If you do not have TI-Nspire Teacher Software to open this file, download the file first, then use the TI-Nspire Document Player to view it without need for purchase or download] The activity will walk students through analyzing their class's data (NOTE: The teacher should note the slideshow at the bottom of this post for pointers as to how this activity is set up. Student weights are "hidden" on the first/title page of this document), as well as a couple of final Self-Check questions to conclude the lesson with a check for understanding.
- GeoGebraTube post for the graph and spreadsheet to display a class's data, showing the Compliant and Non-Compliant regions as they pertain to doctors' recommendations regarding this weight relationship.
Please note the slide show below for images of each of these activity resources with captions to help give pointers as to the intent of the activities as well as user tips and tricks.  Some helpful tips on successfully executing this lesson: - Don't forget to use an accurate scale! I was able to call in a favor with our school's wrestling coach and use their official scale since this lesson happened to fall during their off-season. Especially helpful--since some students were bashful about their data being seen by others--was the fact that the scale had a detachable display screen which could be faced away from their peers.
- Yes, I indulged a bit when using the TI-Nspire CX's (especially since we actually were able to use the CAS version of them). They work great this early in the school year to grab students' attention and quickly engage them in a topic like this one. I otherwise would use a similar activity using the TI-84s we have access to.
- I do not mean to play down the power of GeoGebra in this post. It is a very visual tool and my students have enjoyed it in many other lessons, but it was dependent on me having contained my lesson within a separate file, in this case a PowerPoint. No big deal, but with a couple of network snafus among one of my larger class sizes, I revised last year's lesson plan to instead use the TI-Nspires this time around.
As for the photo at the left of my backpack and the banner above my classroom window (both KELTY, by no coincidence): there's no real rhyme or reason, I just wanted to give a shout out to the company. I still have students who believe I faked both products so that I could dub myself with a pretty sweet nickname. Well, who's laughing when my endorsement deal with them rolls in? Right? Hint, hint... --Keltner-- I mean, Kelty
 As the summer wound down, I found myself frequenting home improvement stores to cross of those last few items on my to-do list. In that wandering, I came across a Giant Jenga topic on a Home Depot Community blog by employees/associates. I figured this would be a great way to tie-in at the beginning of the school year to talk about traits of shapes (in this case squares, so that the Jenga tower has no overlapping from one level to the next). Particularly, I wanted them to address the trait of the assembly that the length of each board was supposed to be the width multiplied by the number of boards stacked across the assembly--in this case, 3 x 5.5" since we went three boards across and each measured 5.5" wide. I was able to toss the idea at the woodworking teacher, who was going to be biding his time in class until students had passed their safety quizzes so they could safely operate the machinery in their shop. He agreed that a straightforward, repetitive project like this one would allow his students to use multiple machines (miter saw, table saw, and planer for example). Before embarking on the project, I made sure to set the scene with my students and pique their interest in creating their own Giant Jenga. They insisted we Google it to see if someone else had already come up with the idea before them. A sweet collection of games came up, but mostly photos, aside from the Home Depot article I'd mentioned above. They noticed it included measurements (i.e. the answer, they thought). I agree with Dan Meyer here: questions like these are most effective when they are un-Google-able.
 Students try out our Giant Genga game as a reward for their efforts. I insisted we go bigger than the Home Depot site had done; we should use 2" x 6" boards instead. The task in class that day was for them to help me make out my shopping list. Some prompts we had to answer: - Why did the Home Depot site mention each board being cut to 10.5" long?
- Would that same length apply when using 2" x 6" boards?
- Could we just buy the longest boards available, or would 8-foot, 10-foot, or 12-foot boards help minimize waste?
- How many, and which length, should I purchase? (When I was at the store, I also discovered the unit rate for these boards differed somewhat; namely that the shorter boards were the cheapest for foot-length. I anticipate revisiting this observation in a later lesson.)
The final product is pictured here. Although it is heavy and not "broken in yet" where the pieces slide easily in and out of their slots, students have enjoyed playing it in the couple of opportunities they have had. The other students from the woodworking class have come by to see the final product in action, since they only saw the raw materials and had not seen the final product in action. I saw recently where Andrew Stadel had posted about an "experienced" Rubik's cube he held onto and a curious student managed to master quickly. While I have a growing collection of Rubik's cubes and similar puzzles (as seen on the banner for this site, atop the shelves in my classroom with Hoberman spheres and other math-y relics), I hope this Giant Jenga game at least makes an impact on these students since they are the ones who came up with the recipe--or the shopping list, I suppose. --Keltner--

This bulletin board is posted outside my classroom to recognize Breast Cancer Awareness Month in October.
Breast cancer affects more people than we easily realize. I learned that this week. As I started to piece this bulletin board display together, a number of passersby made casual comments to the effect of "That's really cool, Mr. Keltner. My ______ (friend, aunt, grandma, father, brother's roommate, and many other examples) is a cancer survivor." If comments like that don't make you glow inside and out, I don't know what to tell you.
After a colleague shared that his mother is a cancer survivor, I'd heard enough. I couldn't just keep all these blessings to myself. I had to share this list of loved ones with others. So, as you can see above, I've begun to accumulate the names of cancer survivors on the four-foot tall pink ribbon adorning the bulletin board.  Nancy and the late Larry Holmes, 2006. I'd like to share a bit about the woman whose name I made sure to include FIRST and foremost on that big ribbon. Her name is Nancy Holmes and I came to know her through a summer job I held with a Full Bright Sign & Lighting, a job that has given me numerous opportunities for real-life math examples in class. It didn't take long to learn that this woman was a fighter, not just advocating to get things done properly and efficiently in the workplace, but that she was a breast cancer survivor. Both breasts. Treated and diagnosed at separate times. Also through this summer job, I came to know Larry. To say he was a gentleman is an understatement. He, too, was a cancer survivor and married Nancy in 2006 after having met during their treatment while each battling cancer. So, when I hear celebrities talk about a "power couple," I know they could not even hold a candle to Nancy and Larry.
 Homecoming King Owen Phariss and his TWO Queens, Audrey Hughes (left) and Rachel Heeb (right). What's more, Nancy's son Owen is her pride and joy. A success story for what someone can do with Down's syndrome (and his mother's strength and determination), Owen was named Homecoming King at his high school during his senior year, a noteworthy occasion not just for him but also for his QUEENS. That's right, the queen voting resulted in an exact tie, so two girls were crowned.So, all the amount of time spent on this bulletin board pale in comparison to the energy Nancy has spent through her fights with cancer. Yes, fights. And while I feel like this bulletin board definitely is something that is Pinterest-worthy, I hope that students, staff, and other passersby are able to soak in the awareness that it is intended for. I hope they are willing to honor a loved one and post their name to acknowledge the fight they have endured. In the meantime, if you have someone whose name you would like me to post on this display among other cancer survivors, send me a comment, a tweet, or an email. Until next time, THINK PINK. --Keltner--
 Slope-R Mario on the scene! When I tried last year to demonstrate slope using GPS receivers, I ran into issues: poor signal, dead batteries, not enough receivers for a BIG class of students, among others.
This year, I tried to do something over the top. The formula that students are familiar with for slope uses m to represent the value of the slope, or rate of change, for the function or relation.
When I looked at the four types of slopes I would be teaching (positive, negative, zero, and undefined slopes), I mashed together examples of their graphs to create a peculiar image, which I later twisted into a logo for a character who visited class.
I managed to make a logo VERY similar to the one on Super Mario's hat in the Nintendo game series!
 Slope-R Mario's logo AND it demonstrated the types of slope I was going to demonstrate in class (with labels placed adjacent to the appropriate line) to help illustrate it to students! I'm not able to hold a candle to Matt Vaudrey's Mullet Lesson, but hoping to have fun trying. He made a much more compelling case for ratios than I think I was able to do. Now, all I needed was a costume to seal the deal. Being so near to Halloween time, I was able to score a Super Mario hat from a neighboring teacher's son, some overalls from the husband of our daycare provider (also a tribute to my high school math teacher, Vern, the focus of this earlier blog post), a mean mustache from the video-editing teacher in my building, and print off a couple of logo medallions to complete my transformation into Slope-R Mario status!
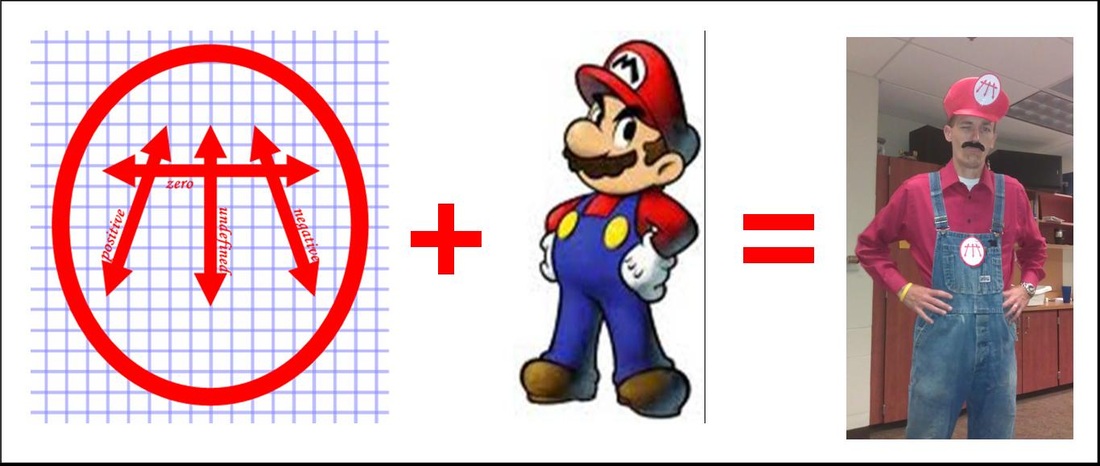
The evolution of my Slope-R Mario idea, coming to life!
I'm attaching screenshots of the notes I used with this lesson. My trademark stick-figure diagrams for types of slope are a favorite from year to year among my students. Simple but effective.
I was also able to insert a collection of images with Super Mario that showed him travelling along paths that incorporated the different examples of slope we were discussing.
Check them out below. So, a good time was had by all. Students got to make fun of me for dressing up so goofily (if that's not a word, it should be and I should trademark it like Anthony Davis trademarked "Fear the Brow" prior to being drafted in the NBA). One side-effect of this lesson I didn't anticipate was seeing students correct their peers when someone interjected a "Mr. Keltner, you're tall and skinny, so you should have dressed up like Luigi!" A bystander was quick to point out "He dressed like Mario because of the 'M' on the logo, since we're doing slope today. It was cool how he made the logo to show the different slopes, right?" The first student agreed, but then quickly retorted "So does this mean when we do parallel and perpendicular lines, THEN you'll dress like Luigi?" Stay tuned and find out. Slope-R Mario, course clear (that's a Nintendo reference). --Keltner--
 How my high school friends picture a math teacher. So, this past Sunday, September 9th, I was named the Region 3 Secondary Level Kansas Teacher of the Year and proceed as one of eight finalists to be considered for Kansas Teacher of the Year. Leading up to this past Sunday's banquet, nominees from the region's school districts were asked to have a 2-3 minute acceptance speech prepared in the event they were named the Finalist for our region. Not expecting to be THAT teacher, I prepared a brief collection of "thank you"s and a short reflection on what brought me to be a math teacher. I promise, the graphic at left will make more sense in a little bit. Anyhow, my acceptance speech went like this: ------------------------------------ First off, I need to thank my wife who is sitting over here...about 24 miles west of here with our daughters, earning more points for her Mother of the Year title. Without her support, I would not be able to do this job I enjoy so much. I am truly a lucky man to have her in my life.I would like to thank Security Benefit for their sponsorship for this recognition program for educators in the state of Kansas and the State Department of Education for their willingness and ability to put on one heck of a party tonight.Well, here goes...Teachers need students, but moreso students need teachers. As the son of two teachers, I have all my life been part of a community of learning. From the Home Economics teacher who plumped me up with a hefty diet of French fries as a toddler--OBVIOUSLY (author's note: I've put on about ten pounds since age 2 and just grown straight up to my tall, lanky stature I currently possess)--to the math teacher who balanced me, and every other teacher's newborn baby, standing upright on his hand like some ill-conceived circus sideshow, I have always been a part of a community of learning.And that math teacher, Mr. Vernon Buell--the one who wore overalls to class on a regular basis and such that I have worn more neckties TONIGHT than he did in his career--served as my vessel by which I was to become a high school math teacher myself.You see, when I graduated high school, my church invited seniors up to the altar to be recognized by the congregation and say a few words about their name, where they planned to attend college, their intended major, and career goals. When it came my turn at the microphone, I stated "Hello, I'm Scott Keltner, I plan to major in mathematics education at Cowley County Community College, and intend to become a math teacher to become the next Vernon Buell."I felt encouraged when a laugh came over the audience, but Vern was serving as an usher that Sunday and stuck his head through the back doors of the sanctuary and boomed loudly "You can try like [heck], boy, but they ain't never made another one like me."How true.And so now, I've found myself as a teacher loving what I do. That love must have rubbed off on my students, as the past two weeks has brought three current and former students to tell me of their plans to become a math teacher themselves, saying they were partly influenced by me.And although I know it would be a stretch of the truth, I'd love to tell THEM "You can try like [heck[, kid, but they ain't never made another one like me."------------------------------------ I think all teachers are somehow influenced by a former teacher we had in class, or encountered somewhere along the way. Vern (my high school math teacher in Medicine Lodge, Kansas) obviously has had some substantial influence on my career path, as well as the stubbornness I think I've acquired over the years. My "Methods of Teaching Mathematics" professor was Dr. Connie Schrock and she made a great impact on some of the habits I have in the classroom, but also managed to coerce me into taking a date to a PTO BINGO Night because she needed volunteers to work the event, saying since I was on the college's tennis team at the time, it would be like having "celebrity BINGO callers." Not being able to find a good enough excuse to get out of it (and having survived the guilt trip when Dr. Schrock accused me of lying that I had a date, which was in itself demeaning enough because it had been a pretty slow semester or two for my love life), I took the date to BINGO Night. Needless to say, that date is not now my wife, although Dr. Schrock did do a good job of talking to her and building me up, saying what a great guy I was among many other great compliments. Or, at least that's what she told me she was saying to her. Nevertheless, if you get a chance to thank a teacher, although today is far away from Teacher Appreciation Day (Tuesday, May 7, 2013 is this year's observance), take the opportunity to tell them how much of an impact they make and how the world can "try like [heck], but they ain't never gonna make another one like them."--Keltner--
|












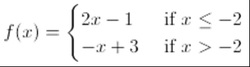
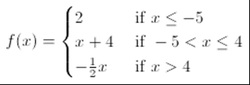









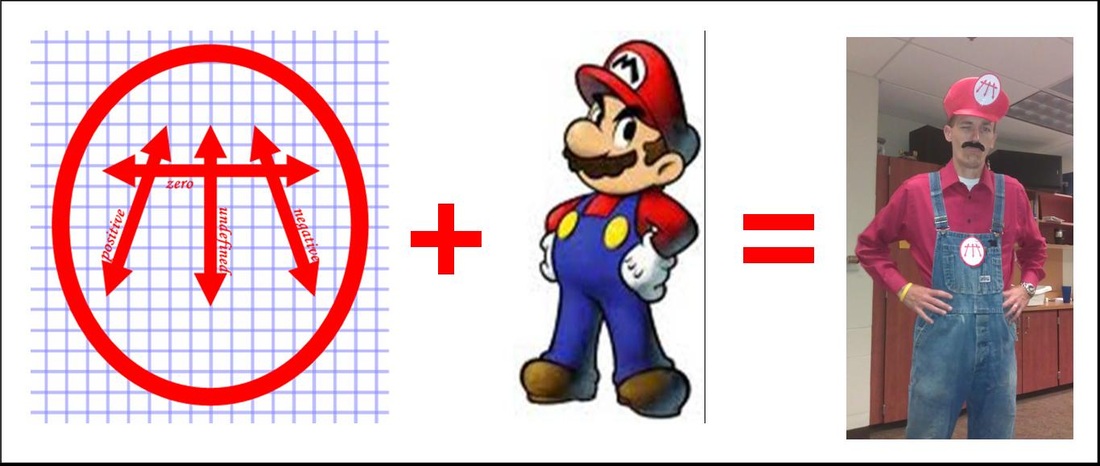

 RSS Feed
RSS Feed