
To elaborate on the picture at the left, our town is working on a grant application through the Kansas Department of Transportation to install a pedestrian bridge over Kansas Highway 10 and seeking community support for the project. You'll understand why this pedestrian bridge relates to the lesson shortly, I swear.

Standard form
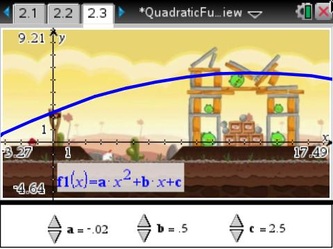
The y = a*x^2 + b*x + c form (yes, this post is letting me see how little formatting I can do with text on my blog), is where our focus began in our quadratics unit. I related this form to the path seen in Angry Birds (shown in the screenshot album below) since the path of the previous shot was visible on screen. I set up sliders to allow students to modify values of a, b, and c and watched them try to map the previous shot they saw. Some comments I heard:
- "Dude, you gotta change c so it's your y-intercept to put the bird in the slingshot!"
- "Yeah, a has to be negative so it's concave down, but make it barely negative so the graph gets wider! Duh!"
- "Whoa, changing the value of b only swivels the graph from side-to-side!" (this was important as we worked later in the unit to factor quadratics)
Most importantly, students were able to connect each constant (a, b, and c) to its unique impact on the shape of the graph, on their own terms--I just used Angry Birds to facilitate the process. The students carried their momentum into Vertex form next.
Vertex form
The y = a*(x - h)^2 + k form, where the vertex is located at (h, k) was a fitting place for me to use Dan Meyer's basketball shot example , because students thus far were struggling with the idea of why symmetry was important in quadratics. They had already aced the idea of wider/narrower graphs and how that was critical to the graph's shape, but I used this to emphasize how each point on one side of the vertex also "secretly" corresponded to another point on the opposite side of the vertex.
Intercept form
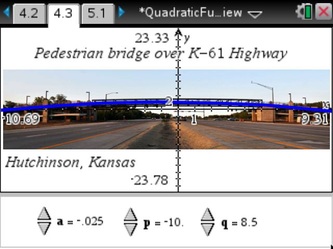
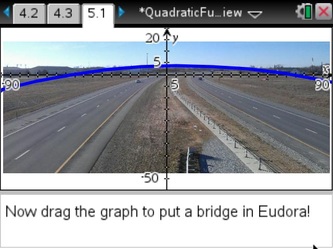
The y = a * (x - p) * (x - q) form that is shown many different ways in many different textbooks. This was going to be the grand finale, bringing in the pedestrian bridge project I'd mentioned earlier (the public information presentation can be found HERE, if you want to know more). I included an example photo of a pedestrian bridge in our state (over Kansas Highway 61 in Hutchinson) and students fit the graph by noting the x-intercepts on the scale that was overlaid on the photo. (Side note: they could also manually enter a value for the constants, they did not need to manually adjust values as small as shown).
Several students also asked about why the towers at each side of the pedestrian bridge had to be so tall, which led us into a side discussion about height clearance and its importance to road traffic that would travel beneath (a decent review of inequalities).
It's fun to have those "I wish my math teacher did things the way you do" moments, with the idea that parents who were at that meeting probably gave their students a pop quiz when they got home without my prompting. Sorry about that, kids.
I'd mentioned a link for the TI-Nspire activity earlier, but HERE it is again if you want to use it or modify it for your own use. Even if you don't have a TI-Nspire handheld, you can give it a test-drive using the TI-Nspire Document Player HERE (open the Doc Player first, then download the activity and open it through the Doc Player interface).
--Keltner--


 RSS Feed
RSS Feed